第二十回 『黄金律と円積法』　　

　太田明氏が百人一首から読み解いたのは10×10の魔法陣で、その中には8×8の魔法陣が内陣していました。その8×8魔法陣こそ長らく失われたとされる、かの易経の秘図、範囲の図という代物でした。　著者はさらにもう一つ、幾何学上の重要な鍵を読み取っています。それが円積法というものです。

　円積法というのは、端的に言えば円と同じ面積の正方形の描き方です。半径１の円の面積はπです。その面積を持つ正方形は一片が√πになります。定規とコンパスだけを用いて、この円と正方形を描く方法、それこそが円積法です。

　無理数πは、なかなか表しにくい。不思議なことに藤原定家らはその円積法をどうやら知っていたのだと思われます。古来から伝わったものかもしれません。

　その方法はずばり、黄金律φを使うものです。彼らはφ２：π＝５：６　という近似値をすでに知っていたようです。誤差は１０万分の１です。黄金律は古くから知られており、幾何学的に簡単に表すことができます。そしてその値は《φ＝（√５＋１）／２》です。正五角形の一片を1とすれば、対角線はφです。

　
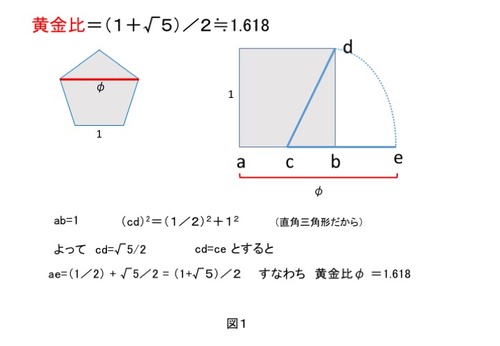
また、一片が1の正方形の下辺の中点から、上辺の右角に斜めに線を引けば、直角三角形ですからその長さは√５／２になります。（△cbd において、cb＝1／２、bd＝１、∴ cd=√5／2）次にその長さをコンパスで弧を描き下辺の延長線との交点をeとします。
正方形の下辺左のac=1／2で、ce=√５／2ですから、ae=(1+√５)／２　となり、黄金律φが書けました。

黄金律が螺旋、フィナボッチ数列などに表れてくることはご存知の通りです。

　さて肝心の円積法ですが、上記の概算式、《φ２：π＝５：６》この式を変えて、φ：√π＝√５：√６　とします。
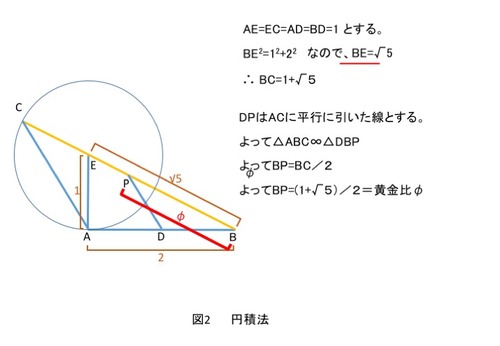
まず√５を書いてみましょう。図2のように横長に直角三角形△ABEを書いてください。AE=１、AB=２とすると、BE=√5になります。
　次にEを中心に半径1の円を描いてください。BEを延長し、円と交わった点をCとします。線ACを引き、それと平行に線DPを描きますが、点Dは、ABの中点です。△ABCは、△DBPと相似になりますので、BPは、BCの１／２です。またBC＝１＋√5 ですから、∴BP=(1+√5)／2 つまり黄金律φです。

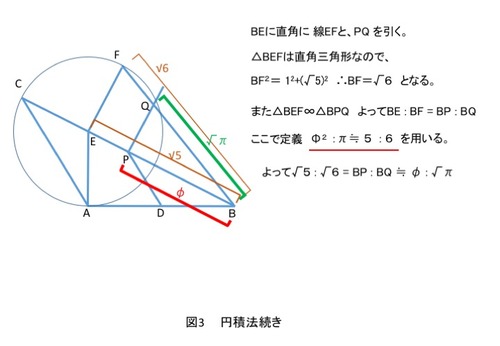
　次に図３のように、BEの上に、直角三角形△EBFを描くと、線BF＝√6になります。また、線EFに平行に線PQを描くと、△PBQができますが、これは△EBFと相似ですね。

　よって、BE:BF=BP:BQ になります。　
さきほどの円積法の近似値（√5：√6=φ：√π）を用いると、BE=√5、BF=√6なので、BQ＝√π となります。
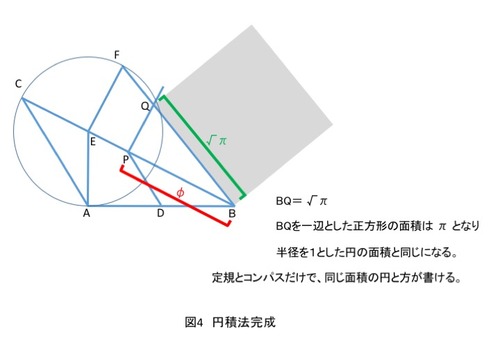
図４のごとく、BQを一片する正方形は、半径１の円の面積と同じπになります。

　円積法はなんと、古代の遺跡、前方後円墳に使われていました。前方の四角と、後方の円の面積を同じにするための手法だったのです。大田明はこの円積法の数が、とんでもないところにも表れていることを発見しました。それは日本の古代遺跡や世界の古代遺跡の距離と配置です。日本の神社や遺跡の位置については既に太陽の道と言われるラインがありました。　...続く

＊著者 プロフィール
なごやかクリニック院長
名古屋醫新の会代表　
岡田　恒良（おかだつねよし）
https://www.facebook.com/tsuneyoshi.okada1
１９５５年岐阜県生まれ
１９８０年岩手医科大学卒
約２０年消化器系一般外科医として通常に病院勤務。市民病院で外科部長として勤務中、ある先輩外科医との運命的出会いがあり、過剰医療や過剰投薬の現状に気づき、自然医学に目覚める。
１９９９年千島喜久男博士の勉強会を名古屋で主催、マクロビオティックの久司道夫氏の講演会企画をきっかけに病院を辞職。
御茶ノ水クリニックの森下敬一博士の機関誌《国際自然医学》に「自然医学の病態生理学」を長期連載。中山武氏の主催するがんの患者会「いずみの会」の顧問をしながら安保徹教授の講演会を開催し、親交を深めた。
看護学校にて補完代替医療について講義中。
２００６年コロンビアのドクトル井上アトム氏に出会い、運動療法・自然療法の重要性を認識。以来南米に３度訪れる。　「自他一如」の探求は２０００年から続く。